3 vejs (2x6.5" + 1x4" + aludome) |
Post Reply 
|
Page <1 7891011 12> |
| Author | ||
bknielsen 
Excentrisk 
Joined: 23 Jun 2009 Location: Midtjylland Online Status: Offline Posts: 603 |
 Quote Quote  Reply Reply
 Topic: 3 vejs (2x6.5" + 1x4" + aludome) Topic: 3 vejs (2x6.5" + 1x4" + aludome)Posted: 26 Feb 2017 at 22:17 |
|
|
Hej Jesper,
Nogle gange kan man få tingene til at gå i fase med et OK frekvensrespons, men med et for højt Q - altså for lav dæmpning (Q=0.5/dæmpningsfaktor), af filterets anden ordens led. Så lyder det ikke godt (synes jeg). Du kan læse om dæmpningsfaktor her: https://en.wikipedia.org/wiki/Damping_ratio. For at tjekke Q (eller dæmpning) udleder du simpelthen overføringsfunktionen ved hjælp ligninger for kondensator: i = C*dv/dt, spole: v = L*di/dt og modstand: v = R*i (Ohms lov) og bruger kirchhoffs lov for strømmen i knudepunkter. Hvis du er helt på bar bund vedr det elektriske, tror jeg, denne side indeholder, hvad du har brug for: http://www.electronics-tutorials.ws/ Differentialerne d/dt erstatter du med s - et bogstav der betragtes som en kompleks variabel, lad være med at tænke over det, hvis ikke du ved, hvad det er. Er du sindssyg nysgerrig så kig her: https://en.wikipedia.org/wiki/Laplace_transform. Herved kan du operere på udtrykkene (gange, dividere, lægge sammen og trække fra), som var de almindelige ligninger. Hvis du f.eks har et tredje ordens filter, udleder du overføringsfunktionen, hvor nævneren bliver et tredje ordens polynomium i variablen s - hvis du har antaget at enheden opfører sig som en simpel modstand - det gør den typisk/næsten ved den frekvens, hvor du tjekker filterets Q (filterets resonansfrekvens). Dit tredje ordens nævner-polynomie i s kan du splitte op i en første ordens del altså (a*s + b) og en anden orden del (c*s^2 + d*s + e). Hermed kan du tjekke Q'et i anden ordensdelen af filteret. Den nemme men ikke nær så sjove løsning: Brug LSPCad hvis du ejer det, og kig på det elektriske frekvensrespons, så er du fri for at tænke. Responset skal ikke have toppe f.eks. lige ved afrulning. Men selv med LSPCad bliver du alligevel let snydt vedr. Q af filtre over anden orden. Det blev måske ikke så kort, men håber det giver mening eller blod på tanden til at prøve det alligevel  . .Edited by bknielsen - 26 Feb 2017 at 22:18 |
||
|
Diskant skal være der, men ikke høres.
|
||
 |
||
USXX 
Pro medlem 
Joined: 17 Dec 2008 Location: Midtjylland Online Status: Offline Posts: 3095 |
 Quote Quote  Reply Reply
 Posted: 27 Feb 2017 at 08:54 Posted: 27 Feb 2017 at 08:54 |
|
Skal det forstås sådan, at du mener, at et Q på 0.5 er for højt?!?
|
||
 |
||
USXX 
Pro medlem 
Joined: 17 Dec 2008 Location: Midtjylland Online Status: Offline Posts: 3095 |
 Quote Quote  Reply Reply
 Posted: 27 Feb 2017 at 09:06 Posted: 27 Feb 2017 at 09:06 |
|
|
M.h.t. til nævnerpolynomiet; man vil ofte omskrive det som:
(s^2 + s*w01/Q + w01^2)*(s+w02), hvor w01 er den naturlige vinkelfrekvens for 2. ordens-leddet, og w02 er den naturlige vinkelfrekvens for 1. ordens-leddet. Q er selvfølgelig Q-værdien for 2. ordens-leddet. For Butterworth kan nævnes, at der for 3. orden gælder, w02=w01 og Q=1. Bemærk, at Q'et ikke er beskrivende for filterets samlede afrulning - det er alene beskrivende for 2. ordensleddet. Edited by USXX - 27 Feb 2017 at 09:08 |
||
 |
||
Jesper_K 
Selvbygger 
Joined: 05 Jun 2015 Location: Odense Online Status: Offline Posts: 19 |
 Quote Quote  Reply Reply
 Posted: 27 Feb 2017 at 10:24 Posted: 27 Feb 2017 at 10:24 |
|
Jeg takker mange gange. Men jeg skal vist lige have gnavet mig igennem det, for at (forsøge) få styr på teorien  Nu var ideen med mit diy projekt at få en forståelse af højttaler og teori, så jeg må bare igang med at læse Nu var ideen med mit diy projekt at få en forståelse af højttaler og teori, så jeg må bare igang med at læse  Mvh Jesper
|
||
 |
||
bknielsen 
Excentrisk 
Joined: 23 Jun 2009 Location: Midtjylland Online Status: Offline Posts: 603 |
 Quote Quote  Reply Reply
 Posted: 28 Feb 2017 at 21:08 Posted: 28 Feb 2017 at 21:08 |
|
Nej bestemt ikke. Jeg skrev bare sammenhængen mellem Q og dæmpningsfaktor: Q = 0.5/dæmpningsfaktor. De bøger, jeg er "opdraget efter", snakker mere om dæmpningsfaktor og tidsrespons, men der er jo en entydig sammenhæng mellem Q og dæmpningsfaktor (Edit: Q faktor har oprindelse i frekvensdomænet - så vidt jeg ved). Et Q på 0.5 er lavt, det svarer jo til kritisk dæmpet, det er nok for meget i den anden grøft. Jeg har lavet 3.ordens diskantfiltre med Q > 1, og nedad. Lige i den konstruktion gav for højt Q stemte s'er - jeg endte med ca. 0.7. Længere ned kunne jeg ikke få fasen til at hænge sammen mellem enhederne - sammen med en OK lydtrykskurve. Har du regnet på Q'et i jeres 2-vejs Satori? De lød i hvert fald virkelig godt til julefrokosten. Det kunne være sjovt at vide, hvad Q'et er i det filter. Måske holder min "teori" om at højt Q ikke lyder godt slet ikke stik  . .Edited by bknielsen - 28 Feb 2017 at 21:24 |
||
|
Diskant skal være der, men ikke høres.
|
||
 |
||
bknielsen 
Excentrisk 
Joined: 23 Jun 2009 Location: Midtjylland Online Status: Offline Posts: 603 |
 Quote Quote  Reply Reply
 Posted: 28 Feb 2017 at 21:10 Posted: 28 Feb 2017 at 21:10 |
|
 |
||
|
Diskant skal være der, men ikke høres.
|
||
 |
||
bknielsen 
Excentrisk 
Joined: 23 Jun 2009 Location: Midtjylland Online Status: Offline Posts: 603 |
 Quote Quote  Reply Reply
 Posted: 28 Feb 2017 at 21:41 Posted: 28 Feb 2017 at 21:41 |
|
...ingen årsag....mon ikke nogle kan anbefale en eller flere rigtig gode bøger skrevet om højtalere, hvis altså du er til rigtige bøger. |
||
|
Diskant skal være der, men ikke høres.
|
||
 |
||
USXX 
Pro medlem 
Joined: 17 Dec 2008 Location: Midtjylland Online Status: Offline Posts: 3095 |
 Quote Quote  Reply Reply
 Posted: 01 Mar 2017 at 08:57 Posted: 01 Mar 2017 at 08:57 |
|
|
@bknielsen; nå, det var det, du mente - undskyld, jeg kunne ikke lige forstå din parentes
 . Ja, Q=1/(2*zeta), hvor zeta er dæmningsforholdet. . Ja, Q=1/(2*zeta), hvor zeta er dæmningsforholdet.Jeg er absolut enig i, at der ikke bør forekomme elektriske resonanser, men når det er sagt, så er der jo mange andre ting, der også skal gå op, før det kommer til at lyde godt. Det er lidt svært at lave en ren/simpel Q-betragtning på ARA-filteret (2-vejs Satori). På diskanten er der godt nok udligning af impedanspuklen ved resonansfrekvensen, så belastningen er så tæt på ren ohmsk, som du kommer. Det var nødvendigt af hensyn til filteret, der kun næsten er 2. orden - det er som udgangspunkt et 2. ordens filter, men der er en relativ stor bund-modstand på spolen. Afrulningen (elektrisk såvel som resulterende akustisk) er ganske blød. På bassen er der baffelkorrektion (hylde-filter) og 2. ordens filter, så belastningen ændrer sig hen over deleområdet (uden baffelkorrektion ville Q'et her være 0.25 og ved max. korrektion ligger vi stadig under 0.7).
Edited by USXX - 01 Mar 2017 at 10:03 |
||
 |
||
bknielsen 
Excentrisk 
Joined: 23 Jun 2009 Location: Midtjylland Online Status: Offline Posts: 603 |
 Quote Quote  Reply Reply
 Posted: 28 Apr 2017 at 22:46 Posted: 28 Apr 2017 at 22:46 |
|
|
Filteret er nu dette, og jeg tror, det er tæt på det endelige. Jeg er kommet frem til, at det er bedst at sætte parallel spolen i mellemtonefilteret nærmest enheden i stedet for lige efter seriekondensatoren.
Selvom man kan opnå god elektrisk dæmpning og stort set samme afrulning med begge konfigurationer lyder nedenstående bare bedre. Seriekondensatoren bliver under halv størrelse og impedansforløbet mere forstærkervenligt. 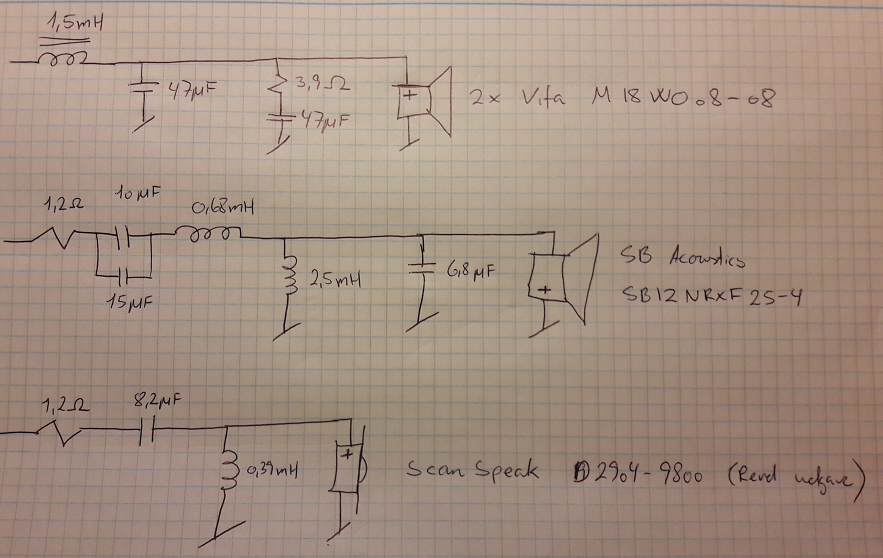
|
||
|
Diskant skal være der, men ikke høres.
|
||
 |
||
USXX 
Pro medlem 
Joined: 17 Dec 2008 Location: Midtjylland Online Status: Offline Posts: 3095 |
 Quote Quote  Reply Reply
 Posted: 29 Apr 2017 at 08:43 Posted: 29 Apr 2017 at 08:43 |
|
|
Det ser ret fornuftigt ud. Hvor krydser bas(ser) og diskant?
Edited by USXX - 30 Apr 2017 at 13:28 |
||
 |
||
Post Reply 
|
Page <1 7891011 12> |
| Forum Jump | Forum Permissions  You cannot post new topics in this forum You cannot reply to topics in this forum You cannot delete your posts in this forum You cannot edit your posts in this forum You cannot create polls in this forum You cannot vote in polls in this forum |